Pythagoras Theorem with all possible Q's at one place

Pythagoras Theorem:

           Case-I (At Right Angle)      Case-II (At Acute Angle)       Case-III (At ObtuseAngle)
                a² = b² + c²                       a² < b² + c²                   a² > b² + c²


The possible quant-comparison Q’s for GRE:
Each question from Q1 to Q5 consists of two quantities, one in column A and one in column B.

You are to compare the two quantities and choose

            A if the quantity in column A is greater;

            B if the quantity in column B is greater;

            C if the quantities are equal;

            D if the relationship cannot be determined from the information given;

Q1)

A 20 foot ladder leaning against a vertical wall with the base of the ladder 10 feet

from wall is pulled 2 feet farther from the wall causing the top of the ladder to

drop x feet.

Column A                      Column B

      X                                  2   

Solution:

Consider right triangle ABC. Let BE = y

Applying Pythagoras theorem at angle B,

(x+y)² + 10² = 20² 

(x+y)²  = 400 – 100 = 300                       - -> (1)

Consider right triangle ABC. Let BE = y

Applying Pythagoras theorem at angle B,

y² + 12² = 20²

y² = 400 – 144 = 256 => y = √256 = 16   - -> (2)

Substituting value of y from (2) in (1),

(x+16)² = 300 => x+16 = √300 => x = √300 – 16

√300 value lies between 17 and 18 (as 17² = 289 and 18² = 324)

Hence x value lies between (17-16) and (18-16) ie., 1 and 2

and must be less than 2. Hence answer option is “A” 

Q2)  Column A          Column B

        AB² + BC²              AC²

Solution:

This is a tricky question. Don’t take it granted that ÐB is 90.

As we have no clues about ÐB or lengths of the sides,

we could not find the relationship between the given columns.

Hence answer option is “D”

Q3)   Column A                   Column B

             X                                  z

Solution:

Observe that ÐB = 90,

Applying Pythagoras theorem at B, z² = x² + y² => z > x

And hence answer option is “B”

Q4) Column A                            Column B

        ÐB                                         90⁰   

Solution:

AC² = 25² = 625; AB² = 20² = 400; BC² = 15² = 225

Observe that AC² = AB² + BC², hence ÐB = 90

And hence answer option is “C”

Q5)  Column A                            Column B

           ÐB                                         90⁰   

Solution:

AC² = 25² = 625; AB² = 22² = 484; BC² = 15² = 225

AB² + BC² = 484+225 = 709

Observe that AC² < AB² + BC², hence ÐB < 90⁰

And hence answer option is “A”

The possible DS section Q’s for GMAT:

Q6 consists of a mathematical problem, and 2 statements containing data.

Then you have to choose one of the 5 different answer choices regarding

which of the 2 statements is sufficient for you to answer the problem.

The answers will be:

A. Statement 1 ALONE is sufficient but statement 2 alone is not sufficient.

B. Statement 2 ALONE is sufficient but statement 1 alone is not sufficient.

C. BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient.

D. EACH statement ALONE is sufficient.

E. Statements 1 and 2 TOGETHER are NOT sufficient.

Q6) In the adjacent figure , what is the length of segment BC?

  (1) x = 90⁰

  (2)The perimeter of △ABC is 40.

Solution:

Using clue (1), applying Pythagoras theorem at angle A,

BC² = 12² + 16² = 144 + 256 = 400 => BC = 20

Using clue (2),

Perimeter = AB + AC + BC = 40 =>12 + 16 + BC = 40

                 =>BC = 40 - 28 = 12

As we could find the solution independently with the clues (1) and (2),

Answer option is “D”

The Possible Problem solving Q’s for all exams:

Q7) The diagonals of a rhombus measure 24 and 10 units. Find the length of sides

of rhombus?

Solution:

In rhombus, diagonals are at right angles and bisect each other.

AB² = OA² + OB² = 12² + 5² 

       = 144 + 25 = 169

=>AB = 13

Q8) The length and width of a rectangle measure 24 and 18 units respectively.

Find radius of circle circumscribing this rectangle?

Solution:

Diagonal of the rectangle is diameter of the circumscribing circle.

AC² = AB² + BC² = 24² + 18² = 576 + 324 = 900

AC = 30 units

AC is diameter of the circle.

=> radius of circle = 30/2 = 15 units

Q9)

Find perimeter of the given parallelogram?

Solution:

Applying Pythagoras theorem at right angle ‘E’,

AD² = DE² + AE² = 3² + 4² = 9 + 16 = 25

AD = 5; BC = AD = 5

AB = CD = DE + EC = 3+5 = 8

Perimeter = AB + BC + CD + AD = 8+5+8+5 =26 

Q10) John walked 6 m east and then 8 m north. How far is he from his starting point?

solution:

Assume that John started at A and walked 6 m east up to B and

then 8 m North up to C.

Distance from the starting point = AC

Applying Pythagoras at right angle B,

AC² = AB² + BC² = 6² + 8² = 36+64 = 100

AC = 10 m

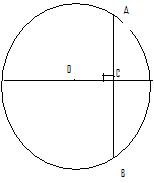
Q11)

Radius of the circle is 5 m and OC = 3 m. Find length of the chord AB?

Solution:

AO = radius = 5  

Applying Pythagoras at right angle C,

OA² = OC² + AC² =>AC² = OA² – OC² = 5² - 3² = 25-9 = 16

=>AC = 4 =>AB = 2 AC = 8 m